Glossario Quantistico

Le parole chiave per scoprire i segreti del Quantum Computing.

Algoritmo Quantistico

Un algoritmo è un procedimento, costituito da un insieme di istruzioni che ci consentono di risolvere un determinato problema (ad esempio calcolare la radice quadrata di un numero). Un algoritmo quantistico è esattamente la stessa cosa, ma le istruzioni consentono anche di creare la sovrapposizione degli stati quantistici e l’entanglement. Questo dà agli algoritmi quantistici la possibilità di eseguire alcuni compiti in un modo molto più efficiente di quanto non si faccia con gli algoritmi classici.

La coerenza quantistica di un qubit è, in termini semplici, la capacità di mantenere la sovrapposizione degli stati nel tempo. E’ l’assenza della ‘decoerenza quantistica’, un processo che porta al collasso degli stati quantistici in stati classici, come ad esempio l’interazione con l’ambiente.

Il computer quantistico a superconduttori (superconducting quantum computer) è una delle possibili implementazioni di un computer quantistico, realizzata con circuiti elettronici superconduttivi. La ricerca nell’ambito dei computer quantistici a superconduttori viene portata avanti da IBM, Google, Rigetti Computing, Microsoft e Intel. I dispositivi sono progettati per lavorare nello spettro delle radiofrequenze (microonde), raffreddati mediante speciali refrigeratori a diluizione sotto i 100 mK e controllati con strumenti elettronici convenzionali (sintetizzatori di frequenze e analizzatori di spettro). Le scale coinvolte (dell’ordine dei micrometri) consentono la progettazione utilizzando le ben note tecniche utilizzate nei comuni circuiti integrati.

Un computer quantistico topologico è un modello teorico di computer quantistico che utilizza delle quasiparticelle in due dimensioni, chiamate anioni, le cui linee di universo passano una intorno all’altra formando delle trecce nello spaziotempo a 3 dimensioni (una dimensione temporale più due dimensioni spaziali). Queste ‘trecce’ costituiscono le porte logiche che costituiscono il computer. Il vantaggio di un computer quantistico basato su queste ‘trecce quantistiche’ consiste nella maggiore stabilità rispetto agli altri modelli teorici di computer quantistici. Piccole perturbazioni possono portare al fenomeno della decoerenza quantistica, introducendo errori nella computazione, che invece non modificano le proprietà topologiche delle ‘trecce quantistiche’. Il modello di computazione quantistica topologica è stato proposto da Alexei Kitaev nel 1997.

Una macchina di Turing quantistica (QTM), detta anche computer quantistico universale, è una macchina astratta utilizzata per creare un modello degli effetti di un computer quantistico. Si tratta di un modello piuttosto semplice che cattura tutta la potenza della computazione quantistica. Qualsiasi algoritmo quantistico può essere espresso, in modo formale, utilizzando una particolare macchina di Turing quantistica. Tali macchine di Turing vennero proposte per la prima volta, in un articolo del 1985 scritto dal fisico David Deutsch della Oxford University. In questo articolo, egli suggeriva che le porte quantistiche potessero funzionare in un modo simile alle porte logiche binarie dei tradizionali computer digitali. Spesso al posto delle macchine di Turing quantistica si utilizzano i circuiti quantistici come modello più comune per analizzare la computazione quantistica; ad ogni modo, entrambi i modelli sono computazionalmente equivalenti.

I criteri di DiVincenzo sono una lista di requisiti necessari per la costruzione di un computer quantistico. La lista è stata proposta dal fisico teorico David P. DiVincenzo nella sua ricerca, pubblicata nel 2000, intitolata “The Physical Implementation of Quantum Computation”. I criteri di DiVincenzo sono costituiti da 5+2 condizioni che un’installazione sperimentale deve soddisfare per poter implementare con successo un algoritmo quantistico, come ad esempio l’algoritmo di ricerca di Grover, o la fattorizzazione di Shor. Le due condizioni aggiuntive sono necessarie per implementare la comunicazione quantistica, come quella utilizzata per la distribuzione della chiave quantistica (QKD).

1 – Scalabilità e qubit ben definiti
2 – Possibilità di inizializzare lo stato dei qubit
3 – Un tempo di coerenza alto
4 – Un insieme universale di porte quantistiche
5 – Possibilità di leggere selettivamente i qubit
6 – Possibilità di convertire qubit stazionari in qubit mobili
7 – Possibilità di trasmettere qubit mobili tra punti specifici

L’effetto tunnel è un effetto quanto-meccanico in cui le particelle hanno una probabilità finita di attraversare una barriera energetica, o di eseguire una transizione ad un stato energetico normalmente proibito dalle leggi della fisica classica. L’effetto è dovuto al comportamentamento ondulatorio delle particelle. L’onda di probabilità di una particella rappresenta la probabilità di trovare la particella in una certa posizione, e c’è una una probabilità finita di trovare la particella dall’altro lato della barriera energetica.

Possiamo considerare l’entanglement quantistico come una connessione speciale tra due qubits. Esistono molti modi per generare il fenomeno dell’entanglement. Un modo possibile è quello di prendere due qubits, avvicinarli, eseguire un processo che li vincoli in un modo speciale ed allontanarli nuovamente. Come esempio concreto possiamo considerare due fotoni emessi da uno stesso atomo quando un suo elettrone discende di due livelli energetici; i fotoni risultanti sono entangled. Quando due qubits sono entangled, anche se vengono allontanati arbitrariamente, resteranno sempre entangled. Il fenomeno dell’entanglement si manifesta chiaramente osservando il risultato della misurazione dei due qubit: la misurazione dei qubit restituirà sempre il valore 0 o il valore 1, in modo totalmente casuale. Ma, indipendentemente dalla loro distanza, quando si misura uno dei due qubit, immediatamente anche l’altro, se misurato, restituirà il medesimo risultato. L’entanglement possiede due proprietà speciali, che sono alla base delle applicazioni pratiche che ne derivano. La prima proprietà consiste nel fatto che l’entanglement non può essere condiviso. Se due qubits sono completamente entangled, nessun altro nell’universo può condividere questo stato speciale. Questa proprietà viene chiamata monogamia dell’entanglement. La seconda proprietà dell’entanglement, che lo rende cosí potente, è chiamata massima coordinazione (maximal coordination). Questa proprietà si manifesta durante la misurazione dei qubits. Se due qubits che sono entangled vengono misurati nella stessa base, non importa quanto siano distanti tra loro, essi restituiranno sempre lo stesso risultato. Questo risultato non è prestabilito, è totalmente casuale, e si concretizza solo al momento della misurazione

Le particelle elementari che costituiscono la materia (i “fermioni”) sono descritte da un’equazione formulata nel 1928 da Paul Dirac, che si chiama appunto equazione di Dirac. Essa prevede che a ogni particella sia associata una relativa antiparticella. Una antiparticella ha le stesse caratteristiche della particella associata tranne la carica, che è opposta; inoltre, se una particella e una relativa antiparticella entrano in contatto, si disintegrano a vicenda liberando energia. Qualche anno dopo, nel 1932, fu scoperta la prima antiparticella: il positrone, associato all’elettrone.L’elettrone e le altre particelle di materia hanno antiparticelle distinte e acquisiscono massa tramite il meccanismo di Higgs: in gergo si parla di “fermioni di Dirac”.
Ed è a questo punto che entra in gioco il fisico italiano Ettore Majorana, che nel 1937 produsse un’equazione simile a quella di Dirac ma più generale (l’equazione di Majorana), che prevede l’esistenza di fermioni neutri (cioè senza carica elettrica) che coincidono con la propria antiparticella.
I “fermioni di Majorana” – così sono stati ribattezzati – sono particelle esotiche perché acquisiscono la loro massa interagendo non con il campo di Higgs ma con se stessi, in quanto sono le loro stesse antiparticelle. Questa interazione può avvenire senza alcuna annichilazione: anzi, i fermioni di Majorana sono molto stabili e interagiscono molto poco con la materia “ordinaria”.

E’ la condizione fondamentale di esistenza, supportata dall’evidenza empirica, in cui un sistema quantistico isolato, come un elettrone libero, non possiede proprietà prefissate fino a quando non vengono osservate in esperimenti appositamente studiati per misurarle. Cioè, una particella non possiede una massa specifica, una posizione, una velocità o uno spin fino a quando una di queste proprietà non viene misurata. Infatti, in senso stretto, la particella non esiste fino a quando non viene osservata.

La misurazione è l’atto di osservare uno stato quantistico. Questa osservazione produrrà, come risultato, una informazione di tipo classico, ad esempio un bit. E’ importante notare che il processo di misurazione altererà in modo irrimediabile lo stato quantistico. Ad esempio, se lo stato quantistico è in sovrapposizione, la misurazione lo farà ‘collassare’ in uno stato classico: zero o uno. Questo ‘collasso’ avviene in modo completamente casuale. Prima della misurazione non c’è modo di conoscere il risultato che si otterrà. Comunque, possiamo calcolare la probabilità di ciascun risultato. Il valore di probabilità costituisce una previsione del risultato della misurazione dello stato quantistico; si tratta di una previsione che possiamo testare più volte, preparando lo stato quantistico molte volte, ripetendo la misurazione, ed infine calcolando la percentuale di ogni possibile risultato.

Sono porte analoghe a quelle utilizzate nei computer convenzionali, anche se differenti da queste ultime per il fatto che seguono le strane regole della meccanica quantistica. Una delle prime realizzazioni di una porta logica quantistica utilizzava una trappola ionica con un singolo atomo di berillio per dimostrare il funzionamento di una una porta logica a due qubit. Un qubit, quello di controllo, è specificato dalle vibrazioni dello ione nella trappola: i due livelli di vibrazione più bassi rappresentano i due valori 0 e 1. L’altro qubit (il target qubit) è specificato dallo stato interno di uno degli elettroni dello ione (spin-down che corrisponde allo stato 0 o spin-up che corrisponde allo stato 1). Inviando degli impulsi laser al singolo ione, si riesce a far funzionare il sistema come una porta C-NOT. Se il qubit di controllo è zero, il target qubit resta invariato; se il qubit di controllo è 1, allora il target qubit inverte il suo valore.

Per uno specifico problema, con questo termine intendiamo il raggiungimento del miglioramento del tempo di esecuzione da parte di un computer quantistico rispetto ad un computer convenzionale che esegue l’algoritmo classico più noto.

I quantum dots sono a tutti gli effetti degli ‘atomi artificiali’. Sono costituiti da nanocristalli di materiale semiconduttore all’interno del quale è possibile intrappolare una coppia elettrone-lacuna. La dimensione nanometrica è comparabile con la lunghezza d’onda della luce, cosí, come capita in un vero atomo, l’elettrone può occupare livelli discreti di energia. I punti quantici (quantum dots) possono essere confinati in una microcavità a cristallo fotonico, dove possono essere controllati con una luce laser.

I computer quantistici sono sempre in contatto con l’ambiente esterno. L’ambiente esterno può disturbare lo stato ‘computazionale’ del sistema, causando la perdita di informazione. La correzione d’errore cerca di combattere questa perdita, prendendo lo stato computazionale del sistema e distribuendolo sullo stato entangled di molti qubits. L’entanglement consente agli osservatori esterni ‘classici’ di osservare e porre rimedio ai disturbi senza però osservare direttamente lo stato computazionale, che in quel caso finirebbe per collassare.

Al QuTech in Olanda, stanno provando a costruire la prima rete internet quantistica del mondo. Una internet quantistica è come la rete Internet che tutti conosciamo, con la differenza che, su quest’ultima è possibile inviare stati quantistici e stabilire l’entanglement tra i vari nodi. Ovviamente costruire una rete internet quantistica globale è molto complesso. In Olanda stanno iniziando a creare una rete costituita da quattro nodi, che nelle previsioni, dovrebbe essere attiva nel 2020. I quattro nodi costituiranno il test per la costruzione di una rete più grande. I quattro nodi della rete saranno in quattro città olandesi: Delft, Amsterdam, Leiden e The Hague.

La distribuzione quantistica della chiave (QKD) è un metodo che sfrutta le proprietà della meccanica quantistica, come ad esempio il teorema di no-cloning, per consentire la comunicazione sicura tra due persone, basata su una chiave crittografica (OTP – One Time Pad). La chiave in questo contesto, è una stringa condivisa solo tra le due persone che desiderano comunicare in modo sicuro. Questa stringa segreta può essere usata per crittografare i messaggi da trasmettere senza che una terza parte sia in grado di decifrarli.

I ripetitori quantistici (Quantum Repeaters) rendono possibile la comunicazione su lunghe distanze in una rete quantistica. Una fibra ottica è in grado di trasmettere un qubit su una distanza approssimativa di 100 chilometri, ma se vogliamo trasmettere ad una distanza maggiore, utilizzare solo una fibra non è sufficiente. Per inviare informazioni su di una distanza maggiore abbiamo bisogno dei ripetitori quantistici. Possiamo pensare ai ripetitori quantistici come ad una serie di piccoli collegamenti tra due punti che sono in entanglement. L’informazione quantistica può essere teletrasportata attraverso questi link ed arrivare con sicurezza a destinazione.

Originatasi in gran parte con la proposta di Richard Feynman del 1982, la simulazione quantistica si è evoluta in un campo di studi a sé, in cui gli scienziati utilizzano un sistema quantistico controllabile per studiarne un secondo, più difficile da gestire sperimentalmente. In sostanza, poiché ancora non esiste un computer quantistico pienamente operativo e scalabile, e i computer classici non sono in grado di risolvere i problemi relativi ai sistemi quantistici, allora i ‘simulatori quantistici’ costituiscono un’interessante attrattiva per ottenere, ad esempio, informazioni sulle proprietà di alcuni materiali complessi

Con questo termine intendiamo il raggiungimento di un punto in cui, un calcolo eseguito su un computer quantistico, non può essere eseguito su nessun computer convenzionale attuale o futuro. Il numero di operazioni richieste alla CPU (e la memoria necessaria) aumentano in modo esponenziale con l’aumentare della dimensione dell’input. Ciò significa che, tranne i casi più semplici, la computazione diventa infattibile su una macchina reale utilizzando solo l’hardware digitale convenzionale.

Un bit classico può trovarsi in uno dei due stati possibili: può essere 0 oppure 1. Un quantum bit, o qubit, può invece trovarsi in uno stato speciale, in cui può essere 0 ed 1 allo stesso tempo: questa particolare situazione è chiamata sovrapposizione degli stati (quantistici). I qubits posseggono un insieme di proprietà peculiari: ad esempio, non è possibile eseguire la copia di un qubit; questa proprietà viene utilmente sfruttata nell’ambito della crittografia quantistica, ma, dall’altro lato rende impossibile utilizzare le tecniche di correzione degli errori che sfruttano la copia.

Un sensore quantistico è un dispositivo che sfrutta la correlazione quantistica (l’entanglement) per raggiungere una sensibilità ed una precisione di misura che non può essere ottenuta con i sistemi classici. Un sensore quantistico misura l’effetto di uno stato quantistico di un altro sistema, su se stesso. Avendo un simile sensore ‘super sensibile’, è possibile misurare i più piccoli effetti immaginabili. Ad esempio, può essere utilizzato per misurare gli effetti delle onde gravitazionali, oppure un piccolo cambiamento in un campo magnetico (anche della Terra stessa), oppure ancora essere utilizzato per costruire dei radar iper sensibili per identificare gli ‘aerei invisibili’

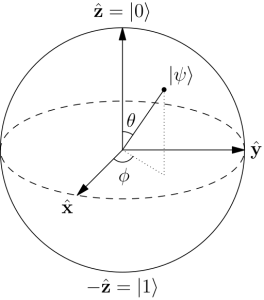
Sfera di Bloch

Sfera di Bloch

In meccanica quantistica, la sfera di Bloch (dal nome del fisico Felix Bloch), è la rappresentazione geometrica dello spazio degli stati puri di un sistema quanto-meccanico a due livelli, il qubit. In altre parole, essa rappresenta gli stati “puri” di un registro quantistico a un qubit. La sfera di Bloch è geometricamente una sfera di raggio unitario i cui punti sulla superficie sono in corrispondenza biunivoca con gli stati “puri” del qubit. Possiamo dare la seguente interpretazione della sfera di Bloch: i poli rappresentano i bit classici, |0⟩ e |1⟩. Questi sono gli unici stati possibili per i bit classici, mentre i qubits coprono l’intera sfera. I qubits contengono molta più informazione dei bit classici, e la sfera di Bloch ce lo mostra graficamente. Quando un qubit viene misurato, collassa in uno degli stati ‘classici’ ai due poli. In quale polo collasserà dipende dalla direzione del vettore che rappresenta lo stato quantistico |ψ⟩. Se la freccia è più vicina al polo nord, c’è una probabilità maggiore che collassi su quel polo. Questo introduce la nozione di probabilità nella sfera di Bloch: l’angolo θ formato dal vettore con gli assi verticali corrisponde a quella probabilità. Se la freccia punta esattamente all’equatore, c’è la probabilità del 50% che collassi in uno dei due poli.

La sovrapposizione degli stati è un principio fondamentale della meccanica quantistica. Possiamo affermare che, come nel caso delle onde nella fisica classica, gli stati quantistici possono essere sommati, cioè sovrapposti, ottenendo un nuovo stato quantistico valido. Al contrario, possiamo dire che ogni stato quantistico può essere considerato come una combinazione lineare (una somma) di altri stati quantistici distinti.

Il teletrasporto quantistico è un metodo per inviare dei qubits utilizzando l’entanglement. Il teletrasporto funziona nel seguente modo (immaginiamo che il teletrasporto avvenga tra due personaggi immaginari, Alice e Bob): per prima cosa Alice e Bob, tra di loro, devono possedere una coppia di qubits in entanglement. Alice prende il qubit che desidera inviare ed il qubit che é in entanglement con il qubit di Bob ed esegue una misurazione. La misurazione provoca il collasso dei qubits e distrugge lo stato di entanglement, ma produce due risultati sotto forma di due bit classici. Alice prende i due bit classici e li invia a Bob mediante la rete Internet classica. Bob applica al suo qubit, un’operazione di correzione che dipende dal valore dei due bit classici ricevuti da Alice. Questa operazione consente a Bob di ottenere il qubit che era posseduto originariamente da Alice. Abbiamo così trasmesso un qubit senza utilizzare alcun mezzo fisico in grado di inviare qubits, ma ovviamente, abbiamo bisogno dell’entanglement per poterlo fare. E’ importante notare che il teletrasporto quantistico non consente la trasmissione ad una velocità maggiore di quella della luce, questo perchè Bob non è in grado di utilizzare il suo qubit prima di aver ottenuto i risultati della misurazione eseguita da Alice. I risultati della misurazione (i due bit classici) impiegano un certo tempo per giungere a Bob, e, la velocità di trasmissione non può essere maggiore di quella della luce.

Il teorema di no-cloning quantistico è una proprietà fondamentale della meccanica quantistica che stabilisce che non è possibile duplicare esattamente (cloning) uno stato quantistico sconosciuto a priori. Questo significa che l’informazione codificata negli stati quantistici è fondamentalmente unica. Questa proprietà è talvolta fastidiosa quando si cerca di proteggere l’informazione quantistica dall’influenza dell’ambiente esterno. Altre volte si rivela molto utile, ad esempio quando decidiamo di stabilire una comunicazione sicura con qualcuno.

Iscriviti su dotQuantum

Entra a far parte del Futuro!!

  • Questo campo serve per la convalida e dovrebbe essere lasciato inalterato.

Cliccando su “ISCRIVIMI” accetti di ricevere la nostra newsletter mensile (Leggi la Privacy Policy). Puoi disiscriverti in qualsiasi momento cliccando sul link nella newsletter che ti invieremo.